Seja V um espaço vetorial sobre um corpo k y q : V → k / [p/pP] uma forma progressiva infinitésima em V. A álgebra de Graceli C(q) é uma álgebra associativa progressional infinitésima sobre k junto com a progressiva V → C(q) definida pela seguinte propriedade universal: para cada álgebra associativa A sobre k com variável função linear j: V → A tal que para cada v em V se tenha j(v)[p/pP] = q(v) [p/pP] (onde [p/pP] denota a identidade multiplicativa de A), há um TRANSmorfismo único da álgebra f: C(q) → A tal que o diagrama seguinte comuta

 [p/pP]

ou seja, de tal forma que fi [p/pP]= j.

A álgebra de Graceli existe e pode ser construída como segue: 

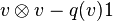 [p/pP]

Se segue desta construção que i é injetivo, e V pode ser considerado como geométrico n-dimensional de C(q) [p/pP] [n-d] [n-dimensões], [cc,cx],sen, cós] [pi].

n-dimensões, côncavo e convexo, sen, cós, pi.

Seja

B(u, v) = q(u + v) - q(u) - q(v) [p/pP][cc,cx],sen, cós] [pi].

a forma multilienar e multiforma do transmorfismo associada a q. Que é uma consequência da definição que a identidade

uv + vu = B (u, v)  [p/pP] [cc,cx],sen, cós] [pi].

vale em C(q) para cada par (u, v) de vetores em V. Se o corpo é de característica [p/pP] distinta de  esta expressão pode ser utilizada como definição alternativa.

A álgebra de Graceli C(q) é filtrada por multiespaço [ver espaço geométrico de Graceli e espaço físicos de Graceli].

o espaço geométrico se caracteriza por formas mutáveis, e o espaço físico por formas mutáveis por agentes físicos, como marés, ventos, radiações, deslocamentos de ar, vórtices, campos, temperaturas, dilatações, e outros.

k ⊂ k + V ⊂ k + V + V [p/pP] [cc,cx],sen, cós] [pi] ⊂ ...

dos elementos que podem ser escritos como polinômios de , [p/pP] [cc,cx],sen, cós] [pi] em V. 

A álgebra de GRACELI associada é canonicamente TRANSmorfa à álgebra Λ V do espaço vetorial. Isto mostra em particular que

dim C(q) = 2^dim V  [p/pP] [cc,cx],sen, cós] [pi].

Uma maneira mais simples de considerar isto é elegendo uma base arbitrária e₁, e₂..... para V. Usando a relação de anticomutação podemos expressar sempre um elemento da álgebra de Graceli como combinação linear de polinômios do tipo

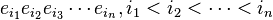 < [p/pP] [cc,cx],sen, cós] [pi].

que resulta num transmorfismo explícito com a álgebra exterior. Observe-se que este é um transmorfismo de espaços vetoriais e de álgebra.